پیش از پرداختن به نمودارهای اساسی جریان ترافیک، لازم است تا با پارامترهای جریان ترافیک آشنا شویم چرا که این نمودارها در واقع روابط بین این پارامترها را نشان می دهند. پارامترهای جریان ترافیک را می توان به دو گروه ماکروسکوپیک و میکروسکوپیک تقسیم بندی کرد. سه پارامتر اصلی ماکروسکوپیک جریان ترافیک، حجم، سرعت و چگالی هستند. پارامترهایی مانند سرفاصله زمانی و سرفاصله مکانی هم در گروه پارامترهای میکروسکوپیک قرار می گیرند.
پارامترهای اصلی جریان ترافیک:
حجم ترافیک:
حجم ترافیک عبارت است از تعداد وسائل نقلیه ای که از یک نقطه از جاده یا یک خط یا جهت مورد نظر از جاده در مدت زمانی مشخص عبور می کنند. با توجه به این تعریف، حجم ترافیک را می توان با واحدهایی مانند خودرو بر ساعت (veh/h) یا خودرو بر ثانیه (veh/s) نشان داد. در این نوشته حجم ترافیک با حرف (q) نشان داده شده است.
سرعت:
سرعت که می توان آن را به صورت کیلومتراژ پیموده شده در ساعت (km/h) یا متراژ طی شده در ثانیه (m/s) نشان داد یکی دیگر از پارامترهایی است که می تواند وضعیت جریان ترافیک را بیان کند. در مهندسی ترافیک دو روش سرعت متوسط زمانی (Time Mean Speed) و سرعت متوسط مکانی (Space Mean Speed) برای محاسبه سرعت متوسط وجود دارد. سرعت متوسط زمانی، سرعت متوسط تمام وسائل نقلیه عبوری از نقطه ای از جاده یا خط عبوری در یک بازه زمانی مشخص است. سرعت متوسط مکانی، سرعت متوسط تمام وسائل نقلیه ای است که در یک بازه زمانی مشخص در محدوده طولی مشخصی از جاده حرکت می کنند. در این مقاله منظور از سرعت، سرعت متوسط مکانی است و با حرف (u) نشان داده شده است.
چگالی:
چگالی جریان ترافیک بیان کننده تعداد وسائل نقلیه در طولی مشخص از مسیر (به عنوان مثال یک کیلومتر) است و واحد هایی مانند تعداد خودرو در کیلومتر (veh/km) می تواند به خوبی مفهوم آن را بیان کند. چگالی با حرف (k) در این مقاله نشان داده است.
رابطه بین جریان، سرعت و چگالی:
همانطور که پیشتر بدان اشاره شد، حجم جریان (q) برابر با تعداد خودروی عبوری (n) از یک نقطه ثابت در یک بازه زمانی مشخص (T) است.
اگر فاصله زمانی بین عبور دو خودروی متوالی از یک نقطه را سرفاصله زمانی (h) در نظر بگیریم، می توانیم رابطه بالا را به صورت زیر بازنویسی کنیم.
چگالی (k) نیز تعداد خودروی موجود (m) در یک طول مشخص از جاده (L) تعریف شد که رابطه ریاضی زیر آن را بیان می کند.
اگر فاصله بین هر دو خودروی متوالی (به عنوان مثال: فاصله بین سپر جلوی خودروی اول با سپر جلوی خودروی دوم) را سرفاصله مکانی (s) در نظر بگیریم، می توانیم رابطه بالا را به صورت زیر بازنویسی کنیم.
حال اگر فرض کنیم تمامی خودروها با سرعت (u) در حال حرکت هستند و سرفاصله های زمانی (h) و مکانی (s) آنها برابر است، رابطه اساسی بین جریان، چگالی و سرعت به صورت زیر محاسبه می شود.
مدل گرین شیلدز
مدل گرین شیلدز یکی از قدیمی ترین روش هایی است که روابط بین پارامترهای جریان ترافیک را بیان می کند. این مدل با فرض وجود رابطه خطی بین سرعت و چگالی به دست آمده است.
در این رابطه نشان دهنده سرعت جریان آزاد و
نشان دهنده حداکثر چگالی یا چگالی اشباع می باشد. با جایگذاری رابطه اساسی به دست آمده بین سرعت، چگالی و جریان در رابطه بالا می توانیم رابطه بین چگالی و جریان را نیز محاسبه کنیم.
شکل زیر نمودارهای اساسی جریان ترافیک را نشان می دهد. همانگونه که مشخص است رابطه بین سرعت و چگالی به صورت خطی است و با افزایش چگالی سرعت کاهش می یابد و با رسیدن به چگالی اشباع به مقدار صفر می رسد. نقطه ای مهم در هر سه نمودار سرعت جریان آزاد است که در شکل با نشان داده شده است. زمانیکه چگالی و یا حجم جریان برابر با صفر باشد، سرعت برابر با سرعت جریان آزاد خواهد بود.
برای محاسبه این سرعت در نمودار دوم که بیان کننده رابطه بین حجم و چگالی است کافیست تا شیب خط مماس بر نمودار را در نقطه مبدا به دست آوریم. این نمودار نشان می دهد که با افزایش چگالی، حجم نیز افزایش می یابد تا به مقدار حداکثر خود برسد، بعد از این با افزایش چگالی، حجم تردد شروع به کاهش می کند تا در چگالی اشباع به مقدار صفر برسد.
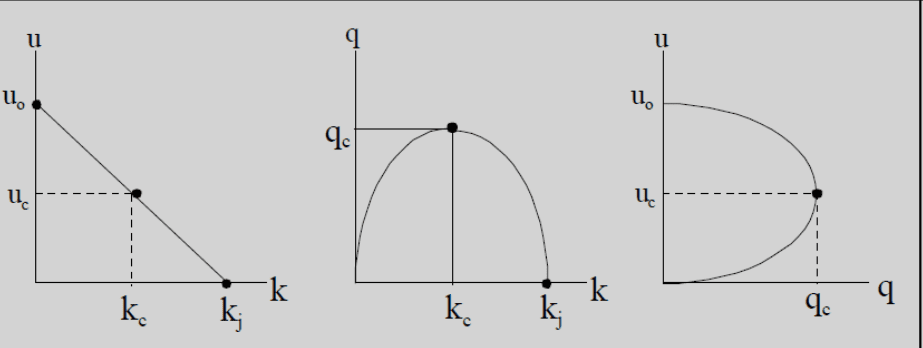
برای محاسبه بیشترین مقدار حجم جریان که با نشان داده شده است، می بایست مشتق رابطه حجم-چگالی نسبت به متغیر چگالی و مشتق رابطه حجم-سرعت نسبت به متغیر سرعت را به دست آورده و برابر با صفر قرار دهیم. به این ترتیب مقادیر چگالی و سرعت را در حالتی که حجم ترافیک در بیشترین حالت خود قرار دارد محاسبه کرده ایم.
مثال:
نمودار اساسی زیر را که رابطه بین سرعت و چگالی برای یک خط از یک آزادراه با و
را در نظر بگیرید.
رابطه بین جریان و چگالی را محاسبه کنید.
مقدار بحرانی چگالی را که باعث بیشینه شدن جریان می شود را تخمین بزنید.
بیشترین مقدار ممکن برای جریان را محاسبه کنید.
مقدار مناسب برای را چنان بیابید که بیشترین مقدار جریان برابر با
گردد.
منابع:
Roess, R. P., Prassas, E. S., & McShane, W. R. (2004). Traffic engineering (pp. 1-99). Pearson/Prentice Hall
Intro to Traffic Flow Modeling and Intelligent Transport Systems

پاسخها