هر گراف شامل مجموعه از گره ها (Nodes) و کمان هایی (Links) است که آنها را به هم متصل می کند. کمان های گراف می توانند جهت دار یا غیر جهت دار باشند. همچنین این امکان وجود دارد که برای هر کمان یک وزن در نظر گرفت.
با توجه به آنچه که گفته شد، شبکه های حمل و نقلی را می توان با استفاده از گراف ها نشان داد. به عنوان مثال می توان به شبکه راه های برون شهری یک کشور اشاره کرد. در این حالت گره ها نشان دهنده شهرها و کمان ها نیز بیان کننده راه های ارتباطی بین شهرها خواهند بود. در شبکه راه آهن نیز می توان ایستگاه ها را به عنوان گره های شبکه و خطوط را به عنوان کمان های شبکه در نظر گرفت. بنابراین می توان هر شبکه حمل و نقل (G) را به صورت زیر در نظر گرفت که در آن (N) مجموعه گره ها و (E) مجموعه کمان ها می باشد.
یکی از مسائل مهم در صنعت حمل و نقل مساله مسیریابی است. کاربرد این مسئله را می توان در بخش های مختلفی از این صنعت مانند تاکسی های اینترنتی و شرکت های توزیع و پخش محصولات مشاهده کرد. میزان اهمیت مسیریابی مناسب در شاخص هایی مانند هزینه تمام شده، زمان تحویل کالا به مشتری و قابلیت اطمینان که همگی می توانند بر موفقیت یک شرکت تاثیر بگذارند، بر کسی پوشیده نیست.
در اینجا می توان به مسئله مهم یافتن کوتاهترین مسیر اشاره کرد که با استفاده از این نوع از الگوریتم ها می توان کوتاهترین مسیر بین هر دو گره را در شبکه یافت. به عنوان مثال یافتن کوتاهترین مسیر بین یک زوج مبدا – مقصد در یک شهر در ساعات اوج ترافیک از کاربردهای این گروه از الگوریتم ها در مهندسی حمل و نقل است.
به صورت کلی می توان الگوریتم های یافتن کوتاهترین مسیر را به دو گروه الگوریتم های تک منبع که کوتاهترین مسیر را از یک مبدا ثابت محاسبه می کنند (Single-Source) و الگوریتم هایی که کوتاهترین مسیر را بین تمام گره ها محاسبه می کنند (All-Pairs) تقسیم کرد. به عنوان مثال الگوریتم دایکسترا از نوع اول و الگوریتم فلوید – مارشال از نوع دوم می باشد.
در این نوشته تمرکز بر روی الگوریتم دایکسترا خواهد بود. در ادامه نحوه کار کردن این الگوریتم توضیح داده می شود و همچنین با ذکر یک مثال به پیاده سازی آن پرداخته خواهد شد.
الگوریتم دایکسترا:
این الگوریتم هم در شبکه های جهت دار و هم در شبکه های غیر جهت دار قابل استفاده است. نکته مهم در مورد استفاده از این الگوریتم پیش نیاز نامنفی بودن وزن های شبکه است. وزن های شبکه می توانند معرف هزینه، زمان یا مسافت بین گره ها باشند.
نحوه عملکرد این الگوریتم به صورت زیر است:
پیش از پرداختن به مراحل کار الگوریتم، نیاز است تا متغیرهای مورد نیاز برای این منظور تعریف و مقادیر اولیه آنها مشخص شوند. در اینجا سه متغیر (dist, Q, S) به شرح زیر تعریف می شوند. اگر نقطه شروع را (O) در نظر بگیریم:
- متغیر (dist) یک آرایه برای ذخیره کردن فاصله نقطه شروع تا سایر گره ها در شبکه خواهد بود. منظور از فاصله نقطه شروع تا سایر گره ها، همان مجموع وزن های کمان ها از نقطه شروع تا هر گره خواهد بود. همانطور که پیشتر نیز گفته شد، وزن هر کمان می تواند فاصله، زمان و یا هزینه سفر بین هر دو گره باشد که در اینجا برای راحتی بیشتر در انتقال مفهوم از فاصله به عنوان وزن هر کمان استفاده می شود.
- نحوه استفاده از این متغیر بدین گونه خواهد بود که برای هر گره، یک عدد را به عنوان فاصله از نقطه شروع ذخیره می کند. به عنوان مثال از آنجایی که فاصله نقطه شروع تا خودش برابر صفر است، برای این گره (dist(O) = 0) خواهد بود. برای سایر گره های شبکه (v) نیز مقدار اولیه را
در نظر می گیریم (
) که در فرایند انجام الگوریتم، با اعداد مناسب جایگزین خواهند شد.
- متغیر (Q) آرایه ای است که در ابتدای فرایند یافتن کوتاهترین مسیر، شامل تمام گره های موجود در شبکه می باشد. در پایان و در زمانی که کار الگوریتم به پایان برسد و کوتاهترین فاصله از نقطه شروع تا تمام گره ها پیدا شود، این آرایه تهی خواهد شد چرا که در هر مرحله، هر گرهی که کوتاهترین فاصله اش تا نقطه شروع پیدا شود، از این آرایه حذف خواهد شد.
- مجموعه (S) نشان دهنده این خواهد بود که کدام گره ها در مراحل یافتن کوتاهترین مسیر، دیده شده اند. منظور از دیده شدن این است که کوتاهترین فاصله از مبدا تا آن گره پیدا شده است. در واقع هر گرهی که از مجموعه Q حذف می شود به این مجموعه اضافه می شود. در پایان و در زمانی که کار الگوریتم به پایان برسد، این مجموعه شامل تمام گره های موجود در شبکه خواهد بود.
با توجه به متغیرهای تعریف شده، مراحل یافتن کوتاهترین مسیر در یک شبکه توسط الگوریتم دایکسترا به صورت زیر خواهد بود:
- گره (v) را به شرطی که هنوز در مجموعه (S) قرار نداشته باشد (کوتاهترین فاصله آن از نقطه شروع پیدا نشده باشد) و دارای کوچکترین مقدار (dist(v)) در میان تمام گره های موجود در مجموعه (Q) باشد، انتخاب می کنیم. واضح است که در ابتدا خود گره شروع (O) انتخاب خواهد شد، زیرا مقدار (dist(O) = 0) می باشد که کمترین مقدار موجود است. این کار تا زمانی که متغیر (Q) تهی نشده است، ادامه می یابد.
- در این مرحله گره (v) به مجموعه (S) اضافه و از مجموعه (Q) حذف می شود.
- حال می بایست تا مقدار متغیر (dist) را برای گره های مجاور گره (v) بروز رسانی کنیم و کمترین فاصله بین آنها تا نقطه شروع را پیدا کنیم. برای هر گره مجاور (u)، اگر رابطه
برقرار باشد، بدین معنی خواهد بود که برای گره (u) یک فاصله کمتر نسبت به مقدار قبلی آن پیدا شده است. به همین دلیل (dist(u)) با مقدار جدید پیدا شده جایگزین می شود. اگر رابطه ذکر شده برقرار نباشد، (dist(u)) بروز رسانی نخواهد شد و مقدار آن در این مرحله تغییر نخواهد کرد.
- الگوریتم به صورت تکراری مراحل بالا را انجام می دهد تا کمترین فاصله مربوط به تمامی گره های موجود در گراف یافت شوند.
در ادامه با ذکر یک مثال نحوه انجام مراحل ذکر شده را بررسی می کنیم. در این مثال سعی داریم تا کوتاهترین فاصله بین گره شماره (0) تا سایر گره ها را بیابیم. اعداد نوشته شده بر روی کمان ها بیانگر فاصله بین هر دو گره می باشد.
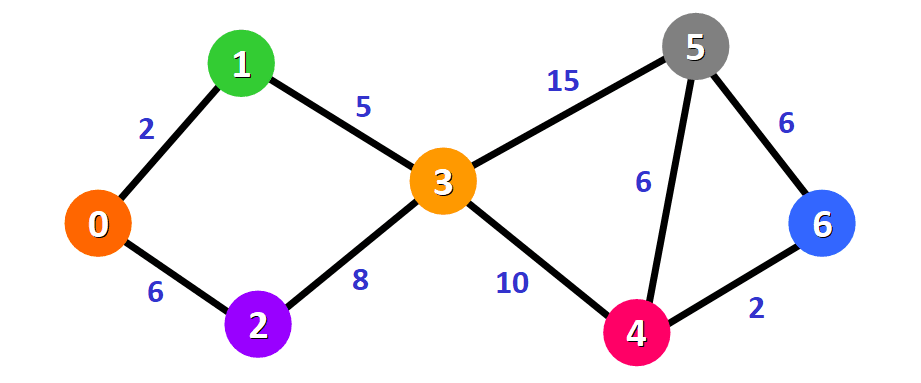
با توجه به آنچه که گفته شد، متغیر (Q) به صورت زیر تعریف خواهد شد. به منظور سهولت، مقادیر مربوط به متغیر dist نیز در این مجموعه نشان داده شده است. همانطور که مشخص است در ابتدا تمامی گره های شبکه در این مجموعه قرار دارند و به غیر از نقطه شروع که فاصله اش برابر با صفر در نظر گرفته شده است، فاصله سایر گره ها تا گره شروع برابر با می باشد. مجموعه (S) نیز در ابتدا تهی خواهد بود.
از آنجایی که گره شروع حرکت، گره (0) می باشد این گره را از مجموعه (Q) حذف می کنیم و به بررسی گره های مجاور آن یعنی گره های شماره 1 و 2 می پردازیم. در این مرحله باید فاصله بین گره های 1 و 2 را با گره مبدا، محاسبه و بروز رسانی کنیم. با توجه به وزن های گراف که درشکل بالا مشخص است، خواهیم داشت:
بعد از انجام بروز رسانی فاصله ها، باید گرهی را که نزدیک تر به گره مبدا می باشد انتخاب کنیم و آن را به لیست گره های دیده شده توسط الگوریتم اضافه کنیم. در اینجا گره شماره 1 انتخاب می شود. بنابراین این گره به همراه گره شروع به مجموعه (S) اضافه می شوند.
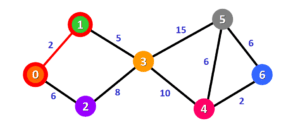
حال مراحل بالا را عینا تکرار می کنیم تا کوتاهترین فواصل سایر گره ها نیز یافت شوند. برای شروع از گره های مجاور گره هایی که در مجموعه (S) قرار دارند شروع می کنیم. گره های مجاوری که باید بررسی شوند، گره شماره 2 و 3 هستند. فاصله مربوط به گره شماره 2 پیش از این پیدا شده بود و نیازی به محاسبه مجدد آن نیست. کوتاهترین فاصله گره شماره 3 تا گره شروع نیز برابر با 7 می باشد.
اکنون که فاصله ها به روز رسانی شده اند، باید گره با نزدیک ترین فاصله به مبدا انتخاب شود. همانگونه که مشخص است از میان گره های شماره 2 و 3، گره شماره 2 دارای فاصله کمتری است. بنابراین این گره از مجموعه (Q) حذف و به مجموعه (S) اضافه می شود.
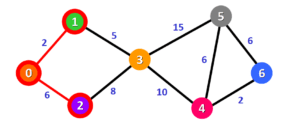
در این مرحله تنها گره مجاور گره های داخل مجموعه (S)، گره شماره 3 می باشد. فاصله مربوط به این گره پیش از این محاسبه و بروز رسانی شده است. در اینجا باید توجه کرد که برای رسیدن به گره شماره 3 از گره مبدا دو مسیر وجود دارد. یک مسیر از گره شماره 1 می گذرد که فاصله ای برابر با 7 دارد و مسیر دیگر از گره شماره 2 می گذرد که دارای فاصله 14 است. از آنجایی که فاصله کنونی کمترین فاصله از مبدا را نشان می دهد نیازی به به روز رسانی نیست. بنابراین تا این مرحله مجموعه های Q و S به صورت زیر خواهند بود:
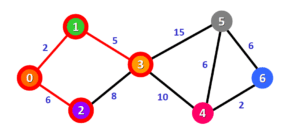
در این مرحله گره های مجاور جدید، گره های شماره 4 و 5 می باشند. همانطور که از شکل قبل مشاهده می شود، کوتاهترین فاصله برای گره شماره 4 برابر با 17 و برای گره شماره 5 برابر با 22 می باشد.
گره شماره 4 از بین گره هایی که هنوز در مجموعه (Q) قرار دارند دارای کمترین فاصله می باشد و بنابراین به عنوان گره جدیدی که به مجموعه (S) اضافه خواهد شد انتخاب می گردد.
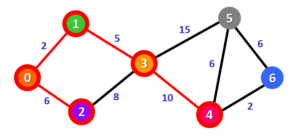
با تکرار مراحل بالا، اکنون باید گره های شماره 5 و 6 مورد بررسی قرار گیرند. برای رسیدن به گره شماره 5، دو مسیر وجود دارد. برای مسیر ، مقدار فاصله برابر با 22 می باشد که در مرحله قبل محاسبه شده است. مسیر جدید با توجه به گره شماره 4، مسیر
خواهد بود که دارای فاصله ای برابر با 23 است. از آنجایی که مقدار قبلی کوچکتر می باشد، فاصله مربوط به این گره همان مقدار 22 خواهد بود. برای گره شماره 6 نیز کوتاهترین مسیر ممکن دارای فاصله 19 می باشد.
با توجه به اینکه فاصله مربوط به گره شماره 6 کوچکتر از گره شماره 5 می باشد، این گره انتخاب شده و به لیست گره های دیده شده (S) اضافه می گردد.
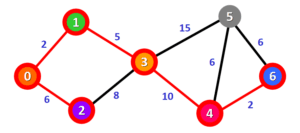
تنها گره باقیمانده گره شماره 5 می باشد. با توجه به شکل بالا برای رسیدن به این گره سه مسیر با فواصل 22، 23 و 25 وجود دارد که همانگونه که پیش از این نیز گفته شد، کمترین فاصله ممکن ملاک انتخاب خواهد بود. با لحاظ کردن گره شماره 5، در پایان کوتاهترین مسیر حرکت از گره شروع یعنی گره شماره صفر تا سایر گره ها به صورت زیر خواهد بود:
منابع:
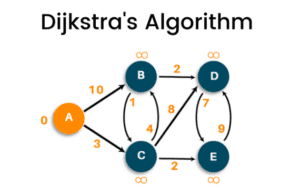
Dijkstra’s Shortest Path Algorithm – A Detailed and Visual Introduction

پاسخها