مقدمه
هزینه حمل و نقل کالا سهم بسزایی در قیمت نهایی آن کالا دارد. لذا بهینه سازی سیستم توزیع کالا از اهداف اصلی شرکت های توزیع کالا است. امروزه، هزاران شرکت و سازمان جمع آوری و تحویل کالا برای کاهش هزینه های عملیاتی و جلب رضایت مشتریان، نیازمند برنامه ای کارا برای ارائه خدمات به مشتریان خود هستند. مسئله مسیریابی وسیله نقلیه، مسئله ای بنیادین در مدیریت توزیع کالا است که تابع هدف و محدودیت های آن در سیستم های توزیع کالا و جابجایی مسافر بر حسب ویژگی های ساختاری و اجرایی سیستم توزیع، متفاوت است. این تفاوت ها منجر به ایجاد طیف وسیعی از مسائل با ویژگی های عملیاتی و ساختاری متفاوت گشته است. علاوه بر این، فارغ از بحث کاربردی بودن این مسئله برای فعالان بخش توزیع کالا، بنیادین بودن آن نیز توجه بسیاری از محققان را در زمینه های مختلف علمی از طراحی الگوریتم و بهینه سازی ترکیباتی تا مدیریت ترافیک به خود جلب کرده است. در نتیجه، ادبیات این مسئله بسیار گسترده و پیگیری روند توسعه و تکامل آن در گذر زمان پیچیده است. بنابراین، بررسی ادبیات مسئله مسیریابی وسیله نقلیه و طبقه بندی مطالعات انجام شده، سرشار از نکات و راهنمایی های علمی و کاربردی است که می تواند برای تحقیقات آتی ارزشمند باشد. در این راستا، در این متن سعی می گردد که ابتدا مسئله فوق تشریح گردد و در ادامه به طبقه بندی مطالعات انجام شده در این زمینه پرداخته می شود.
تعریف مسئله کلاسیک مسیریابی وسیله نقلیه
مسئله مسیریابی وسیله نقلیه (VRP: Vehicle routing problem) از مهمترین مسائل بهینه سازی ترکیباتی است. هدف این مسئله، تعیین مجموعه ای از مسیرها برای خدمت رسانی به مشتریان توسط گروهی از وسائل نقلیه با کمترین هزینه عملیاتی است. اجزای اصلی (VRP)، مشتریان، وسایل نقلیه و دپو هستند.
مشتریان، مجموعه نقاط تقاضا برای دریافت خدمات یا تحویل بار هستند که توسط گروهی از وسائل نقلیه ملاقات می گردند که این وسایل نقلیه، سفرشان را از دپو شروع کرده و به مجموعه ای از مشتریان خدمات می دهند و نهایتاً به دپو باز می گردند.
مراکز اعزام و بازگشت وسائل نقلیه را اصطلاحاً دپو می نامند. در حقیقت، مسئله مسیریابی وسیله نقلیه، ترکیبی از دو مسئله بهینه سازی ترکیباتی : 1) مسئله فروشنده دوره گرد و 2) مسئله پرکردن ظرف است؛ زیرا در مسئله مسیریابی وسیله نقلیه، مشتریان را به گونه ای به وسایل نقلیه اختصاص می دهیم که مجموع تقاضای مشتریان اختصاص داده شده به هر وسیله نقلیه از ظرفیت وسیله نقلیه بیشتر نشود و تعداد وسائل نقلیه کمینه گردد (مسئله پرکردن ظرف). در ادامه، پس از تعیین مشتریان یک وسیله نقلیه، تور بهینه همیلتونی از مشتریان آن وسیله نقلیه را تعیین می نماییم به طوری که هزینه کل کمینه گردد( مسئله فروشنده دوره گرد).
مسئله مسیریابی وسیله نقلیه کلاسیک، به صورت گراف تعریف میگردد که
مجموعه رئوس گراف است و راس های گراف غیر از
، بیانگر مشتری های این مسئله با تقاضای غیر منفی
هستند. راس
، متناظر با دپوی وسایل نقلیه است.
در این مسئله، برای هر یک از یال های گراف G، ، هزینه
را در نظر می گیرند. ماتریس وزن یال ها می تواند متقارن یا نامتقارن باشد و در صورتی که ماتریس وزن یال های گراف متقارن باشد؛ آنگاه مسئله را مسئله مسیریابی وسیله نقلیه متقارن می نامند. هر وسیله نقلیه k دارای ظرفیت
می باشد که از دپو شروع به خدمت رسانی می نماید و در پایان خدمت رسانی دوباره به دپو بر می گردد.
هدف VRP کلاسیک، تعیین مجموعه مسیرهای بهینه است به طوریکه :
- هر مشتری یک و فقط یک بار ملاقات گردد.
- هر وسیله نقلیه از دپو شروع به حرکت می کند و در پایان خدمت رسانی به دپو باز می گردد. به عبارت دیگر، هر مسیر از دپو شروع شده و دوباره به دپو ختم گردد.
- تقاضای کل مشتریان ملاقات شده توسط یک وسیله نقلیه از ظرفیت وسیله نقلیه تجاوز نکند.
برای مسئله مسیریابی وسیله نقلیه کلاسیک، توابع هدف متفاوتی بر اساس نوع مسئله می توان تعریف کرد ولی عموماً، هدف به صورت کمینه کردن هزینه کل به منظور خدمت رسانی به گروهی از مشتریان با تقاضای مشخص بیان می گردد و به صورت یک برنامه ریزی عدد صحیح مرکب مدل می گردد به طوریکه:
در مدل فوق، K تعداد وسایل نقلیه، N تعداد مشتریان، میزان تقاضای مشتری i
،
هزینه حمل بین مشتری های i و j و
متغیر تصمیم گیری است. همچنین رابطه دوم، به ظرفیت هر وسیله نقلیه اشاره دارد. رابطه سوم، بیان می کند که هر وسیله نقلیه از دپو شروع به حرکت می نماید و سرانجام به دپو بر می گردد و در نهایت رابطه چهارم، بیانگر محدودیت تعداد وسائل نقلیه است. شکل های زیر به ترتیب ورودی و خروجی های یک مسئله مسیریابی وسیله نقلیه کلاسیک را نشان می دهد.
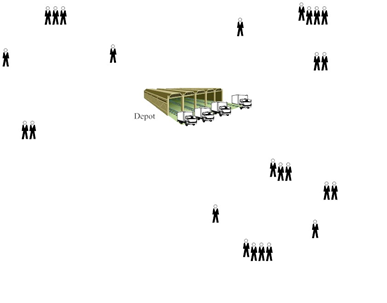
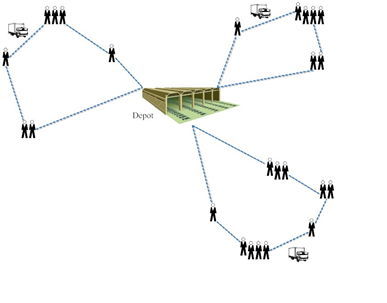
انواع مسئله مسیریابی وسیله نقلیه
تابع هدف و محدودیت های مسئله مسیریابی وسیله نقلیه در سیستم های توزیع کالا و جابجایی مسافر بر حسب ویژگی های ساختاری و اجرایی سیستم توزیع، متفاوت است. این تفاوت ها منجر به ایجاد طیف وسیعی از مسائل با ویژگی های عملیاتی گوناگونی گشته است که در این قسمت سعی می شود تا تعدادی از اصلی ترین انواع توسعه یافته مسئله کلاسیک مسیریابی وسیله نقلیه تبیین و به صورت اجمالی تشریح شوند.
مسئله مسیریابی وسیله نقلیه با چندین دپو
امروزه بسیاری از شرکت های توزیع کالا از چندین دپو برای جمع آوری یا توزیع کالا استفاده می نمایند؛ زیرا به کارگیری یک دپو برای توزیع کالا در محدوده خدمت رسانی از دیدگاه اقتصادی مقرون به صرفه نیست. مسئله مسیریابی وسیله نقلیه با چندین دپو (MDVRP)، شکل کلی مسائلی را در بر می گیرد که در آن از چندین دپو برای خدمت رسانی به مشتریان استفاده می شود. در این مسئله، هر وسیله نقلیه از یک دپو حرکت می نماید و پس از ملاقات مشتریانش دوباره به همان دپو بر می گردد.
این مسئله دارای سه مرحله تصمیم گیری می باشد. در مرحله اول هر مشتری به یک دپو اختصاص داده می شود و مشتریان گروه بندی می گردند، سپس به مشتریان یک گروه، وسیله نقلیه ای اختصاص داده می شود و در نهایت، نحوه و ترتیب ملاقات مشتریان توسط یک وسیله نقلیه مشخص می گردد. شکل زیر، حل یک مسئله مسیریابی وسیله نقلیه با چندین دپو را نشان می دهد.
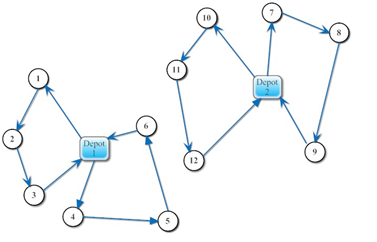
مسئله مسیریابی وسیله نقلیه با کالای برگشتی
مسئله مسیریابی وسیله نقلیه با کالای بازگشتی (VRPB)، نوعی از مسائل مسیریابی را شامل می شود که در آن مشتریان علاوه بر اینکه کالاهایی را دریافت می کنند می توانند بعضی کالاها را به دپو باز گردانند. مثلا فرض کنید که در یک کارخانه تولیدی لازم است که محصولات تولید شده در بین مشتریان توزیع شوند، همچنین مواد اولیه مورد نیاز کارخانه نیز از تامین کنندگان مواد اولیه، به کارخانه حمل شود به طوریکه که در هر لحظه مجموع مواد توزیعی و مواد اولیه دریافت شده از تامین کنندگان کمتر از ظرفیت وسیله نقلیه باشد و هر مشتری دریافت کننده یا تامین کننده کالا، یک و فقط یک بار و تنها توسط یک وسیله ملاقات گردد.
مسئله مسیریابی وسیله نقلیه با پنجره های زمانی
مسئله مسیریابی وسیله نقلیه با پنجره های زمانی (VRPTW)، یکی از مهمترین و کاربردی ترین انواع VRP است. این مسئله، توسعه یافته «مسئله مسیریابی وسیله نقلیه کلاسیک» است که در آن هر مشتری در یک بازه زمانی معین (پنجره زمانی) ملاقات می گردد؛ در نتیجه، سرویس دادن به مشتری قبل از این پنجره زمانی منجر به اضافه شدن یک زمان انتظار در کل زمان سفر می شود.
به عبارت دیگر، خدمت رسانی به هر مشتری i باید در یک بازه زمانی صورت گیرد. در حقیقت، یک وسیله نقلیه اگر قبل از زمان
به مشتری i برسد باید تا زمان
صبر کند، همچنین خدمت رسانی به این مشتری نباید بعد از زمان
انجام گیرد.
مسئله مسیریابی وسیله نقلیه باز
هدف مسئله مسیریابی وسیله نقلیه باز (OVRP)، تعیین مسیرهای بهینه برای مجموعه ای از وسائل نقلیه به منظور خدمت رسانی به تعدادی مشتری مشخص است به طوری که هر وسیله نقلیه از دپو، سفرش را شروع می نماید ولی در پایان خدمت رسانی به دپو باز نمی گردد. در حقیقت اصلی ترین تفاوت بین مسئله کلاسیک VRP و OVRP در نوع مسیرها می باشد؛ در VRP هر مسیر یک تور همیلتونی است در حالیکه در OVRP هر مسیر یک مسیر همیلتونی است. شکل زیر، یک حل شدنی مسئله مسیریابی وسیله نقلیه باز را نشان می دهد.
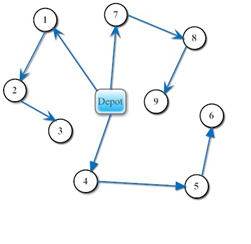
مسئله مسیریابی وسیله نقلیه احتمالی
مسئله مسیریابی وسیله نقلیه احتمالی (SVRP)، توسعه یافته مسئله کلاسیک مسیریابی وسیله نقلیه است که در آن برخی از اجزا و مولفه های مسئله کلاسیک را احتمالی در نظر می گیرند. سه مولفه اصلی که در مسئله مسیریابی می توان احتمالی در نظر گرفت به صورت زیر است:
- مشتریان احتمالی : در این حالت مشتری i با احتمال
حاضر است و با احتمال
غایب می باشد.
- تقاضای احتمالی: تقاضای فرد i،
، یک متغیر تصادفی است.
- زمان احتمالی یا هزینه احتمالی: در این حالت، زمان سفر یا هزینه یال های گراف به صورت یک متغیر تصادفی در نظر گرفته می شود.
مسئله مسیریابی وسیله نقلیه احتمالی، در مسائل واقعی همچون پخش مواد غذایی، جمع آوری پول از شعبه های بانک و سایر خدمات جمع آوری و تحویل کالا کاربرد دارد.
مسئله مسیریابی وسیله نقلیه فازی
در مسئله مسیریابی وسیله نقلیه فازی (FVRP)، از تئوری های مجموعه فازی برای مدلسازی عدم قطعیت های موجود در این مسئله استفاده می شود. در مطالعات گذشته عموماً عدم قطعیت در موارد ذیل را مورد توجه قرار داده اند:
- عدم قطعیت در تقاضا: در این حالت تقاضا را به صورت یک عدد فازی تعریف می نمایند.
- عدم قطعیت در هزینه یا زمان بین دو مشتری: در این حالت، هزینه یال گراف بین دو مشتری را ثابت در نظر نمی گیرند؛ بلکه از اعداد فازی برای نمایش این هزینه استفاده می شود.
روشهای حل
مسئله مسیریابی وسیله نقلیه یکی از مسائل بهینه سازی ترکیباتی می باشد. در تئوری پیچیدگی محاسباتی ثابت شده که این مسئله از مسائل سخت (NP-Hard) است و برای آن الگوریتم حل با مرتبه زمانی چند جمله ای وجود ندارد. لذا، زمان حل مسئله مسیریابی وسیله نقلیه با افزایش تعداد گره ها به صورت نمایی افزایش می یابد. در دهه های گذشته الگوریتم های مختلفی برای حل این مسائل ارائه شده است. این روش ها را می توان به دو دسته کلی روش های دقیق و روش های تقریبی تقسیم بندی نمود.
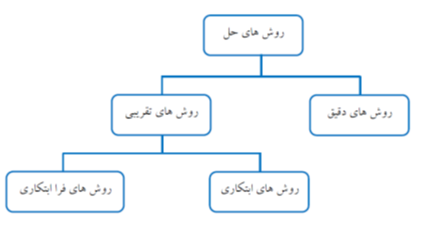
روش های حل دقیق بر پایه مفاهیم تحقیق در عملیات هستند و بهینه جهانی را برای مسئله تعیین می نمایند و برای مسائل با اندازه کوچک موثرند، ولی با بزرگ شدن اندازه مسئله، روش های دقیق قادر به تعیین جواب بهینه در زمان قابل قبول نیستند. تعداد این الگوریتم ها و تنوع آنها نسبت به روش های ابتکاری اندک است. از متداول ترین روش های حل دقیق، می توان به دو روش شاخه -کران و روش شاخه – هزینه اشاره کرد.
دسته دوم روش های حل مسئله مسیریابی وسیله نقلیه، الگوریتم های تقریبی هستند. این الگوریتم های جواب هایی نزدیک به جواب بهینه در یک زمان قابل قبول ارائه می دهند که به دو دسته فرعی الگوریتم های ابتکاری و الگوریتم های فرا ابتکاری تقسیم بندی می گردند. از الگوریتمهای فراابتکاری میتوان به الگوریتم ژنتیک، مورچگان، جستجوی ممنوع اشاره کرد. با توجه به گستردگی روشهای حل، خواننده محترم جهت آشنایی با روشهای حل، میتواند به مراجع انتهای متن رجوع نماید.
نرم افزارهای رایگان جهت حل مسائل VRP
در زمینه حل مسائل VRP چندین نرم افزار رایگان وجود دارد که میتوان به موارد زیر اشاره کرد:
کتابخانههای حاوی مسائل نمونه
جهت ارزیابی الگوریتمهای حل، اغلب از یکسری مسائل نمونه و استاندارد استفاده میشود. برخی از کتابخانه حاوی مسائل نمونه به شرح ذیل است:
منابع
Braekers, K., Ramaekers, K., & Van Nieuwenhuyse, I. (2016). The vehicle routing problem: State of the art classification and review. Computers & industrial engineering, 99, 300-313
Toth, P., & Vigo, D. (Eds.). (2002). The vehicle routing problem. Society for Industrial and Applied Mathematics
Mor, A., & Speranza, M. G. (2022). Vehicle routing problems over time: a survey. Annals of Operations Research, 314(1), 255-275
Eksioglu, B., Vural, A. V., & Reisman, A. (2009). The vehicle routing problem: A taxonomic review. Computers & Industrial Engineering, 57(4), 1472-1483
Liu, T., Jiang, Z., Liu, R., & Liu, S. (2011). A review of the multi-depot vehicle routing problem. Energy Procedia, (13), 3381-3389


پاسخها