تاریخ انتشار: 12 مرداد 1401
تاریخ ویرایش: آذر 5, 1402
نویسنده: modir1
No Comments

روش بیشینه درستنمایی

چکیده: برای برآورد پارامترهای یک مدل آماری چندین روش منجمله روش بیشینه درستنمایی، مساوی قراردادن ممان‌ها و غیره وجود دارد. در این نوشته، روش بیشینه درست‌نمایی و کاربرد آن برای برآورد پارامترهای مدل لوجیت همراه با یک مثال تشریح می‌شود.

روش بیشینه درستنمایی متداول‌ترین رویه در تخمین پارامترهای یک مدل انتخاب گسسته بر اساس نمونه‌ای از دادههای مشاهداتی است به طوری که در آن مقادیر پارامترهای مدل به گونه‌ای تخمین زده می‌شود که احتمال رخ دادن نمونه مشاهده شده، بیشینه شود.

در صورتیکه با مدل های انتخاب گسسته آشنایی ندارید، می توانید با مراجعه به مقالات پیشین این مجموعه در مورد مبانی مدل های انتخاب گسسته، مدل های لوجیت و پروبیت مطالعه کنید.

فرض کنید $\displaystyle \left\{ {\left. {({{\mathbf{x}}_{n}},{{y}_{n}})|n=1,...,N} \right\}} \right.$ مجموعه مشاهدات در یک نمونه باشند به طویکه مشاهدات از جامعه به صورت تصادفی و مستقل انتخاب شده باشند. در اینصورت تابع درستنمایی $\displaystyle L$ به صورت زیر تعریف می‌شود:

$\displaystyle L(\mathbf{\theta })=\prod\limits_{{n=1}}^{N}{{f({{y}_{n}}|{{\mathbf{x}}_{\mathbf{n}}},\mathbf{\theta })}}$

که در آن $\displaystyle f({{y}_{n}}|{{\mathbf{x}}_{\mathbf{n}}},\mathbf{\theta })$ احتمال شرطی $\displaystyle {{y}_{n}}$ به شرط $\displaystyle {{\mathbf{x}}_{\mathbf{n}}}$ و $\displaystyle \mathbf{\theta }$ بردار پارامترها است.

در ادبیات مدل‌های انتخاب مسیر گسسته متداول است که به جای بیشینه کردن تابع درستنمایی، لگاریتم آن را بیشینه نمایند. زیرا تابع لگاریتم، تابعی اکیداً صعودی است و در نتیجه، این عمل در مقادیر بهینه بردار پارامترهای مدل ( $\displaystyle \mathbf{\hat{\theta }}$ ) تاثیری ندارد به طوریکه می توان نوشت:

با توجه به اینکه $\displaystyle LL$ ، تابعی غیرخطی است لذا جواب بهینه این تابع باید شرایط درجه اول را ارضاء نماید؛ به عبارتی دیگر

$\displaystyle \frac{{\partial LL}}{{\partial {{{\hat{\theta }}}_{k}}}}=0$

در رابطه فوق، $\displaystyle {{\theta }_{k}}$ ، k امین عضو مقادیر بهینه بردار پارامترها $\displaystyle \mathbf{\hat{\theta }}=\left\{ {\left. {{{{\hat{\theta }}}_{1}},...,{{{\hat{\theta }}}_{k}},...,{{{\hat{\theta }}}_{K}}} \right\}} \right.$ است.

لازم به ذکر است که برای ارزیابی نیکویی برازش مدلهای تخمین زده شده توسط روش بیشینه کردن درستنمایی، از معیار $\displaystyle {{\bar{\rho }}^{2}}$ استفاده میشود که تا حدودی نقشی شبیه به $\displaystyle {{R}^{2}}$ در ارزیابی نیکویی برازش مدلهای رگرسیونی ایفا می‌نماید؛ به طوریکه:

$\displaystyle {{\bar{\rho }}^{2}}=1-\frac{{L(\mathbf{\hat{\theta }})-K}}{{L(0)}}$

که در آن، $\displaystyle L(0)$ بیانگر مقدار تابع درستنمایی است هنگامی که مقادیر همه پارامترها در تابع درستنمایی برابر با صفر در نظر گرفته شود. شاخص $\displaystyle {{\bar{\rho }}^{2}}$ بین 0 تا 1 تغییر می‌کند و بیانگر بهبود در مقدار لگاریتم تابع درستنمایی نسبت به شرایطی است که همه پارامترهای مدل، صفر در نظر گرفته شوند. لذا، هر چه مقدار شاخص فوق بیشتر باشد، مدل مناسب‌تر است. به بیانی دیگر، در مقایسه دو مدل که مجموعه گزینه‌های انتخاب آن یکسان و از یک‌ مجموعه داده برای پرداخت مدل‌ها استفاده شده باشد، مدلی که $\displaystyle {{\bar{\rho }}^{2}}$ بیشتری دارد، مناسب‌تر خواهد بود.

همچنین در ارزیابی مدل‌های انتخاب گسسته، از آزمون t-test برای بررسی فرض صفر بودن یک پارامتر و از شاخص $\displaystyle \xi =-2\left( {L(0)-L(\mathbf{\hat{\theta }})} \right)$ برای برسی فرض صفر بودن تمامی پارامترها استفاده می‌شود. شایان ذکر است که شاخص $\displaystyle \xi$ دارای توزیع کای دو با K (تعداد پارامترهای مدل) درجه آزادی است. برای آشنایی بیشتر با روش بیشینه درست‌نمایی، در ادامه یک مثال در زمینه برآورد پارامترهای مدل لوجیت پرداخته می‌شود.

فرض شود داده ‌های جدول زیر مشاهدات حاصل از یک آمارگیری باشند. قصد داریم با داده های جدول زیر یک مدل لوجیت برای انتخاب شیوه سفر بین اتوبوس و خودروی شخصی بسازیم.

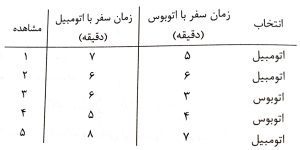
فرض شود که تابع مطلوبیت اتوبوس و سواری شخصی به صورت زیر باشند:

$\displaystyle {{V}_{{car}}}={{\beta }_{0}}+{{\beta }_{1}}{{t}_{car}}$

$\displaystyle {{V}_{{bus}}}={{\beta }_{1}}{{t}_{{bus}}}$

بر اساس مشاهدات و روش بیشینه درستنمایی، تابع ذیل باید بیشینه شود:

$\displaystyle \begin{array}{l}L=\left( {\frac{{\exp \left( {{{\beta }_{0}}+7{{\beta }_{1}}} \right)}}{{\exp \left( {{{\beta }_{0}}+7{{\beta }_{1}}} \right)+\exp \left( {5{{\beta }_{1}}} \right)}}} \right)\left( {\frac{{\exp \left( {{{\beta }_{0}}+6{{\beta }_{1}}} \right)}}{{\exp \left( {{{\beta }_{0}}+6{{\beta }_{1}}} \right)+\exp \left( {6{{\beta }_{1}}} \right)}}} \right)\times \\\quad \left( {\frac{{\exp \left( {3{{\beta }_{1}}} \right)}}{{\exp \left( {{{\beta }_{0}}+6{{\beta }_{1}}} \right)+\exp \left( {3{{\beta }_{1}}} \right)}}} \right)\left( {\frac{{\exp \left( {4{{\beta }_{1}}} \right)}}{{\exp \left( {{{\beta }_{0}}+5{{\beta }_{1}}} \right)+\exp \left( {4{{\beta }_{1}}} \right)}}} \right)\left( {\frac{{\exp \left( {{{\beta }_{0}}+8{{\beta }_{1}}} \right)}}{{\exp \left( {{{\beta }_{0}}+8{{\beta }_{1}}} \right)+\exp \left( {7{{\beta }_{1}}} \right)}}} \right)\end{array}$

همانطور که پیش‌تر بیان شد، برای آسانی کار از دو طرف رابطه فوق لگاریتم می گیریم. سپس مشتق جزیی LL نسبت به پارامترهای مجهول را محاسبه و برابر با صفر قرار می دهیم. به عبارتی دیگر:

$\displaystyle \frac{{\partial LL}}{{\partial {{\beta }_{0}}}}=0$