مدلهای انتخاب گسسته بر مبنای تئوری مطلوبیت تصادفی بنیان نهاده شدهاند. تئوری مطلوبیت تصادفی، یکی از تئوری های اقتصادی است که در آن فرض بر آن است که هر فرد سعی مینماید انتخابی که ماکزیمم مطلوبیت را به همراه دارد به عنوان گزینه انتخابی خود برگزیند.
فرض شود که بردار مطلوبیتهای متناظر با مجموعه
عضوی گزینههای انتخاب باشد. مطلوبیت هر یک از گزینههای انتخاب برای یک تصمیمگیر،
، تابعی از مشخصهها و ویژگیهای مشاهده شده هر یک از گزینهها و ویژگیهای مشاهده شده آن تصمیمگیر است. این شاخصها و ویژگیهای مشاهده شده هر یک از گزینههای انتخاب با بردار
نمایش داده میشود. لذا تابع مطلوبیت گزینه
را میتوان به صورت
نمایش داد.
به منظور دخیل کردن شاخصها و ویژگیهای مشاهده نشده هر یک از گزینهها، مطلوبیت هر گزینه انتخاب، به صورت یک متغیر تصادفی در نظر گرفته میشود که این متغیر تصادفی از مولفه قطعی و مولفه تصادفی
تشکیل شده است. مولفه تصادفی در حقیقت بیانگر ویژگیهای مشاهده نشده گزینههای انتخاب و تفاوت بین مطلوبیت ادراک شده توسط تصمیم گیر و مطلوبیت واقعی گزینههای انتخاب است. بنابراین مطلوبیت گزینه انتخاب
به صورت زیر بیان می گردد:
در مدلهای انتخاب گسسته، احتمال انتخاب گزینه ام از بین مجموعه گزینههای انتخاب به صورت زیر تبیین میشود:
در رابطه فوق، تابع انتخاب ، تمام ویژگیهای واقعه تصادفی را دارد به طوری که:
واضح است که احتمال انتخاب گزینه ،
، وابسته به نوع تابع چگالی احتمال عبارت خطا
است. در مدلهای انتخاب گسسته، عموماً، تابع چگالی احتمال خطا را نرمال یا گامبل فرض مینمایند. فرض تابع چگالی احتمال گامبل برای عبارت خطا، منجر به مدل لوجیت و فرض تابع چگالی احتمال نرمال برای عبارت خطا، منجر به مدل پروبیت میشود.
در عمل، بکارگیری مدل لوجیت برای مسائل واقعی نسبت به مدل پروبیت متداولتر است؛ زیرا، پرداخت مدل های لوجیت و برآورد پارامترهای آن با استفاده از روشهایی همچون بیشینه درستنمایی بسیار آسانتر از مدل پروبیت است.
در ادامه، برای درک بهتر موارد فوق، به یک مثال پرداخته میشود. فرض شود بین دو ناحیه یک شهر دو شیوه سفر وجود دارد: 1) خودرو شخصی و 2) اتوبوس. مطلوبیت شیوههای سفر به صورت ذیل است:
در روابط فوق منظور از t زمان سفر و منظور از c هزینه سفر است. فرض شود بین زوج مبدا و مقصد مفروض، زمان سفر با اتوبوس و اتومبیل به ترتیب برابر با 25 دقیقه و 20 دقیقه و هزینه سفر با اتومبیل و اتوبوس به ترتیب برابر با 3 و 2 واحد باشد. اگر متغیر جزءهای تصادفی از هم مستقل باشند و توزیع آنها یکنواخت بین 1- تا 1 باشد، احتمال انتخاب هر گزینه را به صورت زیر میتوان محاسبه کرد.
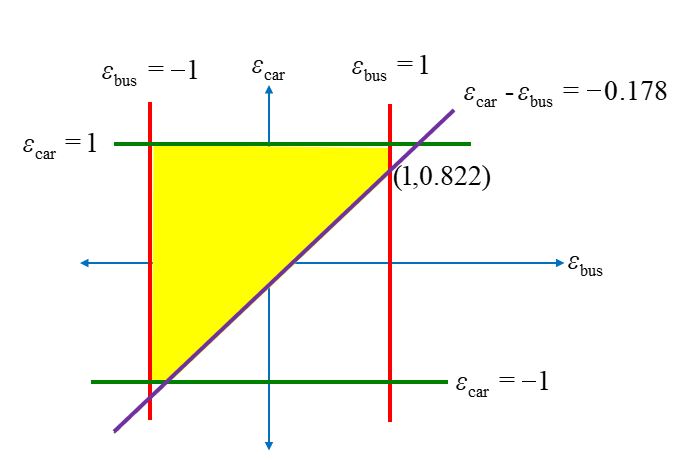
برای محاسبه احتمال پیشامد فوق، با توجه به اینکه متغیرهای تصادفی از نوع یکنواخت هستند، احتمال متناظر با مساحت فضای پیشامد به مساحت فضای نمونه (4 واحد) است. در شکل زیر فضای متناظر با پیش آمد فوق با رنگ زرد متمایز شده است. مساحت بخش زرد رنگ برابر با 2.34 و مساحت فضای نمونه برابر با 4 است. لذا، احتمال انتخاب خودروی شخصی برابر با 0.59 و به تبع آن درصد استفاده از خودروی شخصی 59 درصد است.
در ادامه این مبحث به مدل های انتخاب گسسته لوجیت و مدل های پروبیت پرداخته خواهد شد.


پاسخها