تاریخ انتشار: 10 خرداد 1402
تاریخ ویرایش: آبان 10, 1402
نویسنده: modir1
No Comments

آزمون های فرضیه

چکیده: آزمون فرضیه شکلی از استنتاج در آمار است که به وسیله آن فرضی در مورد پارامتر جامعه بررسی می شود. روش استفاده شده به ماهیت داده های مورد استفاده و هدف تجزیه و تحلیل بستگی دارد. آزمون فرضیه با توجه به داده ها، شواهدی در مورد قابل قبول بودن فرضیه ارائه می دهد.

فرض کنید به عنوان یک مهندس ترافیک با بالا بودن سرعت متوسط خودروها در یک معبر رو به رو هستید. از شما خواسته می شود تا راهکارهایی ارائه دهید تا سرعت در این معبر کاهش یابد. شما در قدم اول در یک برداشت میدانی سرعت متوسط کنونی را اندازه گیری می کنید که در اینجا آن را ( $\displaystyle {{\mu }_{b}}$ ) می نامیم. سپس راهکارهایی از قبیل نصب تابلوی محدودیت سرعت و استفاده از سرعت گیر را پیشنهاد کرده و آنها را اجرا می کنید. پس از آن مجددا سرعت متوسط ( $\displaystyle {{\mu }_{a}}$ ) را برداشت می کنید. حال سوالی که پیش می آید این است که آیا پس از عملیاتی شدن راهکارهای ارائه شده، سرعت متوسط کاهش یافته است. برای پاسخ دادن به این سوال از آزمون های فرضیه استفاده می شود که در ادامه به بررسی آن می پردازیم و مفاهیم مرتبط با فرض های آماری، سطوح معناداری و P-value را مورد بررسی قرار می دهیم.

فرض های آماری:

فرض صفر (( $\displaystyle {{H}_{0}}$ ) Null hypothesis) فرضی است که نشان می دهد هیچ تفاوتی بین گروه های مورد مطالعه وجود ندارد. در مثال مطرح شده به معنای این می باشد که سرعت متوسط قبل و بعد از عملیاتی شدن راهکارهای کاهش سرعت تفاوتی نکرده است.

$\displaystyle {{H}_{0}}:{{\mu }_{b}}={{\mu }_{a}}$

به صورت پیش فرض، فرض بر این است که فرض صفر معتبر می باشد و سعی بر آن است تا با جمع آوری اطلاعات لازم این فرض رد شود.

فرض جایگزین (( $\displaystyle {{H}_{a}}$ ) Alternate Hypothesis) فرضی است که بیان کننده وجود تفاوت بین گروه های مورد مطالعه است. در مثال مطرح شده، فرض جایگزین نشان دهنده به وجود آمدن تفاوت در سرعت متوسط بعد از اعمال تغییرات است. در این مثال می توانیم فرض جایگزین را به دو صورت تعریف کنیم. در حالت اول سرعت ها با هم برابر نیستند و در حالت دوم سرعت پس از اعمال تغییرات کاهش یافته است.

$\displaystyle {{H}_{a}}:{{\mu }_{b}}\ne {{\mu }_{a}}$

$\displaystyle {{H}_{a}}:{{\mu }_{a}}<{{\mu }_{b}}$

هر زمان که سعی بر رد کردن یا پذیرفتن فرض ها داشته باشیم، این امکان وجود دارد که دچار اشتباه شویم و دو خطای عمده زیر اتفاق بیافتد.

فرض صفر به اشتباه، رد شود. با توجه به اینکه فرض صفر بیان کننده عدم وجود تفاوت است، وقوع این خطا بیان می کند که بین گروه های مورد مطالعه تفاوت وجود دارد، در حالی که بین آنها تفاوتی نیست. در مثال مطرح شده رد کردن فرض صفر به معنای پذیرفتن این است که سیاست های اعمال شده برای کاهش سرعت اثرگذار بوده و سرعت ها متفاوت شده است. این خطا را خطای نوع اول می نامند و آن را با $\displaystyle \alpha$ نشان می دهند.

فرض صفر به اشتباه، رد نشود. این به این معناست که زمانی که می بایست فرض صفر رد شود، به اشتباه پذیرفته شده است و در حالیکه بین گروه های مورد مطالعه تفاوت وجود دارد، به اشتباه می پذیریم که بین آنها تفاوت وجود ندارد. وقوع این خطا در مثال مطرح شده نشان می دهد که راهکار های اعمال شده برای کاهش سرعت موثر نبوده است. این خطا را خطای نوع دوم می نامند و آن را با $\displaystyle \beta$ نشان می دهند.

سطح معنی داری:

سطح معنی داری ( $\displaystyle \alpha$ ) در واقع میزان خطایی است که در رد کردن فرض صفر مرتکب می شویم. به عنوان مثال اگر سطح معنی داری را 5 درصد در نظر بگیریم، به این معناست که تا 5 درصد مواقع اشتباه رد شدن فرض صفر را می پذیریم.

P-value:

هنگام بررسی داده ها این احتمال وجود دارد که تحلیل های ما نسبت به فرض های مطرح شده دارای سو گیری باشد. در مثال مطرح شده در بالا، این امکان وجود دارد که تحلیل ها به صورتی انجام شود که نشان دهنده وجود تغییرات در سرعت (در اینجا کاهش سرعت) پس از سرمایه گذاری های انجام شده باشد. در این مثال تفاوت سرعت برداشت شده در مطالعه قبل و بعد ( $\displaystyle {{\mu }_{b}}-{{\mu }_{a}}$ ) می تواند دو حالت داشته باشد. این تفاوت می تواند واقعی باشد و یا صرفا یک نویز تصادفی باشد که ناشی از ناکافی بودن نمونه های جمع آوری شده است. برای پی بردن به اینکه کدام یک از این دو مورد صحیح است، از (P-value) استفاده می کنیم.

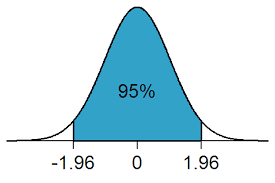
P-value به ما می گوید که با فرض درست بودن فرض صفر، احتمال مشاهده داده ها به چه شکل است. برای فهم بهتر به شکل زیر که توزیع نرمال را نشان می دهد، دقت کنید. اگر سطح معنی داری را 0.05 در نظر بگیریم، 95 درصد داده ها در بازه بین $\displaystyle [-1.96,1.96]$ قرار می گیرند. با فرض برقرار بودن فرض صفر، اگر داده ای در این بازه قرار بگیرد ( $\displaystyle p>0.05$ )، تعجب آور نیست. اما اگر داده ای در خارج از محدوده یاد شده قرار بگیرد ( $\displaystyle p<0.05$ )، نیاز به بررسی بیشتر دارد.

این شکل سطح معنی داری 5 درصد را نشان می دهد.

محققان معمولا به دنبال نشان دادن صحت تئوری مطرح شده توسط خود هستند، ولی وقتی مقدار P-value محاسبه می شود تنها می توان راجع به داده ها صحبت کرد. این مهم است که بدانیم که P-value به احتمال مشاهده داده ها مربوط است و ارتباطی با احتمال درست بودن یک تئوری ندارد. بنابراین می توان P-value را این گونه تفسیر کرد که داده های مشاهده شده تا چه میزان با فرض صفر مطرح شده همخوانی دارند. مقادیر پایین P-value به معنای عدم وجود همخوانی و مقادیر بالای آن به معنای وجود همخوانی بیشتر است. به همین دلیل است که مقادیر پایین P-value باعث رد کردن فرض صفر می شود و مقادیر بالای آن به معنای عدم توانایی در رد کردن فرض صفر خواهد بود. برای درک بیشتر به شکل زیر توجه کنید.

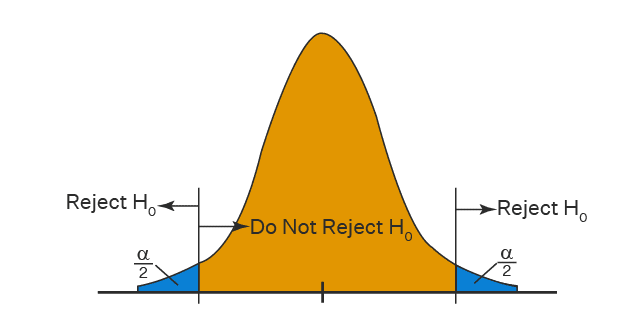
رد کردن یا رد نکردن فرض صفر — در این شکل ارتباط بین سطح معنی داری و پذیرفتن یا رد کردن فرض صفر نشان داده شده است.

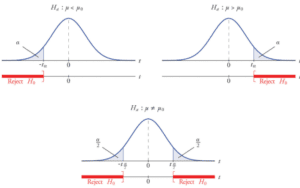
برای تفسیر P-value از سطح معنی داری استفاده می شود. اگر $\displaystyle p<\alpha$ باشد می توان فرض صفر را رد کرد و این به معنای وجود تفاوت آماری معنادار بین گروه ها می باشد. در مثال مطرح شده در ابتدای بحث می تواند به معنای تغییر سرعت متوسط خودروها پس از اعمال اصلاحات لازم باشد. اما اگر رابطه $\displaystyle p>\alpha$ برقرار باشد، نمی توان فرض صفر را رد کرد و می توان آن را این گونه تفسیر کرد که تفاوت معنادار آماری بین گروه ها وجود ندارد. لازم به ذکر است که عدم رد شدن فرض صفر به معنای عدم وجود تفاوت نیست و ممکن است با در اختیار داشتن تعداد نمونه بیشتر بتوان فرض صفر را رد کرد.

منابع:

p-values: What they are and how to interpret them

Null Hypothesis, p-Value, Statistical Significance, Type 1 Error and Type 2 Error

Improving your statistical inferences

Roess, R. P., Prassas, E. S., & McShane, W. R. (2004). Traffic engineering (pp. 1-99). Pearson/Prentice Hall

Vous devez être connecté pour noter

نویسنده:

برچسب ها: hypothesis test, p-value, آزمون های فرضیه, برداشت میدانی, خطای نوع اول, خطای نوع دوم, سطح معنی داری, فرض جایگزین, فرض صفر, مطالعات قبل و بعد

لینک کوتاه:

پاسخ‌ها

پورتال مهندسی راه و حمل و نقل
(سایت تپ)

سایت تپ بستری پویا برای همکاری و تبادل نظرهای تخصصی، آموزش، اطلاع‌رسانی، همچنین شناخت و حمایت از استعدادها، در حوزه حمل و نقل است.

در نسخه آزمایشی سایت تپ اساتید دانشگاه، دانشجویان، متخصصین و مسئولین حوزه حمل و نقل می‌توانند:

ضمن معرفی توانایی‌ها و حوزه‌های تخصصی خود، تعامل نزدیک‌تر، دوستانه‌تر و مؤثرتری با یکدیگر داشته باشند
از مطالب آموزشی ارائه شده از طرف سایت تپ یا سایر کاربران استفاده کنند، یا مطالب مفید خود را با دیگران به اشتراک بگذارند
از رویدادهای علمی و آکادمیک حمل و نقلی ایران و جهان آگاه شوند
از اخبار صنعت حمل و نقل در ایران و جهان مطلع شوند
به منابع مفید شامل کتب، آئین‌نامه‌ها و نقشه‌های مرتبط با حمل و نقل و راه‌سازی دسترسی داشته باشند.
درخواست تهیه منابع مورد نظر خود را بدهند

در نسخه اصلی سایت تپ (نسخه 1.0 و بالاتر) که در آینده نزدیک رونمایی خواهد شد، خدمات بسیار متنوع‌تر و کامل‌تری در اختیار کاربران عزیز قرار خواهد گرفت. علاوه بر امکانات طراحی شده از طرف تیم علمی و اجرایی سایت تپ، که به مرور زمان به سایت اضافه خواهند شد، کاربران عزیز می‌توانند امکانات و خدمات مورد نیاز خود را اعلام کنند، تا بررسی و در صورت امکان به لیست خدمات اضافه شوند.

کوتاه سخن آن که می‌‎خواهیم در کنار هم با مشارکت فعال، بهره‌گیری از دانش جمعی، آموزش و دانش‌افزایی در حوزه حمل و نقل تحول آفرین باشیم.

انتشار مطالب با ذکر منبع بلامانع است.

© حقوق محفوظ است.

عضویت در کانال تلگرام